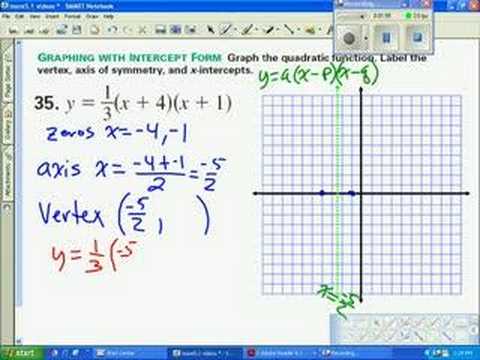
So the vertex of the parabola is, \[(h,k)=(2,2)\], So the vertex form of the above parabola is, \[y=a(x-2)^2+2\,\,\,\rightarrow (1)\]. Note in particular the difference in the $(x-h)^2$ part of the parabola vertex form equation when the $x$ coordinate of the vertex is negative. This vertex of a parabola calculator displays a vertex and standard form of the given equation. Thus, the standard form of the given parabola is: Here are a few activities for you to practice. \right)\\[0.2cm] &= 2 \left(\!\! Now, replace the blank space on either side of our equation with the constant 9: Next, factor the equation inside of the parentheses. Now, there are a couple of ways to go from here. For example, y=(x-2)(x+4). Remember: in the vertex form equation, $h$ is subtracted and $k$ is added.


eNotes.com will help you with any book or any question. Then, we can calculate the f(x) to find out the y-coordinate of a vertex. The difference between a parabola's standard form and vertex form is that the vertex form of the equation also gives you the parabola's vertex: $(h,k)$. To turn this into standard form, we just expand out the right side of the equation: Tada! Ask questions; get answers. Check this out. If you need to find the vertex of a parabola, however, the standard quadratic form is much less helpful. From this form, it's easy enough to find the roots of the equation (where the parabola hits the $x$-axis) by setting the equation equal to zero (or using the quadratic formula). For example, take a look at this fine parabola, $y=3(x+4/3)^2-2$: Based on the graph, the parabola's vertex looks to be something like (-1.5,-2), but it's hard to tell exactly where the vertex is from just the graph alone. Estimate the values of parameter: \( b = 2 ah and c = a h^2 + k \). Hint: write all Latest answer posted July 01, 2015 at 6:16:49 AM. 2.y=0.8(1.28)^x

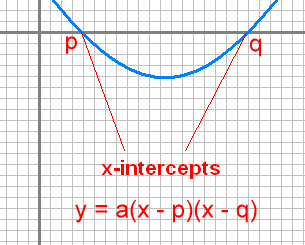
Instead, you'll want to convert your quadratic equation into vertex form. Apply the following formulas to find the values the values of \(h\) and \(k\) and substitute it in the vertex form (\(y=a(x-h)^2+k\)). Write an equation in vertex form: \( m = a (x h)^2 + K. \), Now, expand the square formula: \( m = a (x^2 + y^2 + 2hx) + K. \), Multiply the inner side or bracket: \( a x^2 + a y^2 + 2 ahx + K. \), Then, compare with quadratic form of a parabola: \( m = a x^2 + b x + c. \). #3: Given the equation $y=2(x-3/2)^2-9$, what are the $x$-coordinates of where this equation intersects with the $x$-axis?
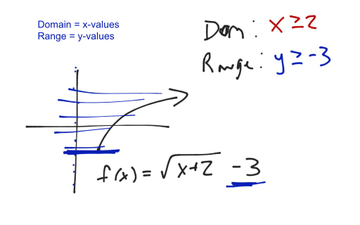
 form intercept change slope standard jquery
form intercept change slope standard jquery Latest answer posted December 13, 2012 at 12:39:15 AM.
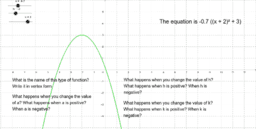
Our summaries and analyses are written by experts, and your questions are answered by real teachers. (If your $a$ value is 1, you don't need to worry about this.). section of this page to learn more about it.

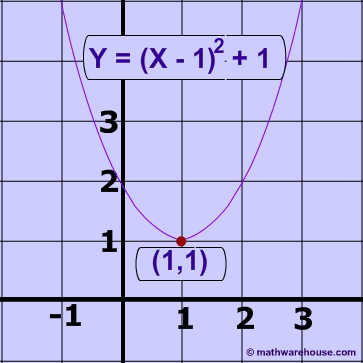
Read on to learn more about the parabola vertex form and how to convert a quadratic equation from standard form to vertex form. The first thing you'll want to do is move the constant, or the term without an $x$ or $x^2$ next to it. Whew, that was a lot of shuffling numbers around! How do you write #y+1=-2x^2-x# in the vertex form?
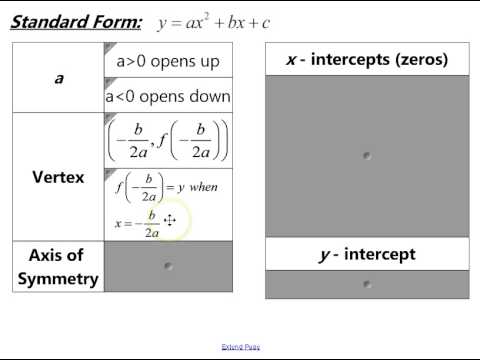
y&=-3(x+1)^{2}-6\\[0.2cm]
(I think about it as if the parabola was a bowl of applesauce; if there's a $+a$, I can add applesauce to the bowl; if there's a $-a$, I can shake the applesauce out of the bowl.).
 quadratic intercept quadratics attending
quadratic intercept quadratics attending A turning point is a point where the parabola is upward (from decreasing to increasing) and f(x)=0 at the point. Be it worksheets, online classes, doubt sessions, or any other form of relation, its the logical thinking and smart learning approach that we, at Cuemath, believe in. or, in a simpler representation,
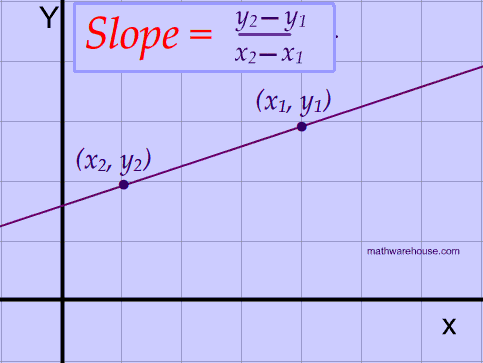
slope intercept form equation line write points mx lines using examples graph equations intro example 3x katesmathlessons constant where math To find the vertex, the x coordinate is the average of the zeros; substitute this value for x to get the y coordinate. around the world. So to convert the standard form to vertex form, we just need to complete the square. -----------------------------------------------------------------------------. Add and subtract it after the \(x\) termin (1): \[2 x^{2}\!+\!7 x\!+\!6 = 2\left(\!\!x^2 \!+\! If the radius of a circle is doubled, what effect does this haveon the area of the circle? For f(x) =x^2 +6x +8, determine the vertex, axis of symmetry, intercepts, domain, range, intervals where the function is increasing and decreasing and the graph. \((h,k)= \left(-\dfrac{7}{4},-\dfrac{1}{8}\right)\). Here y=(-1-2)(-1+4)=(-3)(3)=-9 so the vertex is at (-1,-9).
slope form intercept standard converting convert freeware unknown thursday april posted Step 1: Identify the coefficient of \(x\).

The 5 Strategies You Must Be Using to Improve 4+ ACT Points, How to Get a Perfect 36 ACT, by a Perfect Scorer. All rights reserved. She scored 99 percentile scores on the SAT and GRE and loves advising students on how to excel in high school. This equation is looking much more like vertex form, $y=a(x-h)^2+k$. A Comprehensive Guide.
shmoop thegriftygroove intercepts How doI determine if this equation is a linear function or a nonlinear function?

#2: Convert the equation $7\bi y=91\bi x^2-112$ into vertex form. Our new student and parent forum, at ExpertHub.PrepScholar.com, allow you to interact with your peers and the PrepScholar staff. How to Convert Standard Form to Vertex Form: How to Convert Vertex Form to Standard Form: How we can find the turning point of a function? In other words, #alpha# and #beta# are solutions to an equation If you want to know how to change the vertex to standard form, lets start! First, we'll move the constant over to the left side of the equation: Next, we'll divide both sides of the equation by 2: Now, the sneaky part. Let us know your assignment type and we'll make sure to get you exactly the kind of answer you need.
 intercept form graph vertex parabolas axis symmetry standard study forms
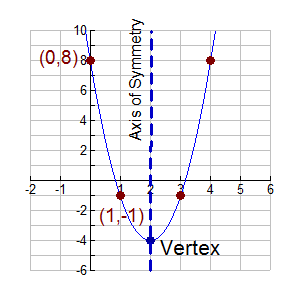
intercept form graph vertex parabolas axis symmetry standard study forms Because we completed the square, you will be able to factor it as $(x+{\some \number})^2$. On the circumference? More to the point, the axis is the arithmetic mean of the two zeros.
See if you can solve the problems yourself before reading through the explanations! How Do You Calculate It? So to convert the standard to vertex form we need to complete the square. Normally, you'll see a quadratic equation written as $ax^2+bx+c$, which, when graphed, will be a parabola. Let us convert the equation \(y=-3(x+1)^{2}-6\) from vertex to standard form using the above steps:
intercept form parabolas lesson How do you graph quadratic equations written in vertex form? The process of converting your equation from standard quadratic to vertex form involves doing a set of steps called completing the square. Use this vertex form calculator to find the vertex and y-intercept points of the given equation. We always struggled to serve you with the best online calculations, thus, there's a humble request to either disable the AD blocker or go with premium plans to use the AD-Free version for calculators. While the standard quadratic form is $ax^2+bx+c=y$, the vertex form of a quadratic equation is $\bi y=\bi a(\bi x-\bi h)^2+ \bi k$. y&= -3(x+1)(x+1)-6\\[0.2cm]
In the conic section, the vertex form of a parabola is a point or place where it turns, it is also known as a turning point. Ask below and we'll reply! To find \(a\) here, we have to substitute any known point of the parabola in this equation. #-x^2+8x-12=0# Step 2: Make it half and squarethe resultant number. If the above process seems difficult, then use the following steps: Here is the "Standard Form to Vertex Form Calculator.". y&=-3x^2-6x-9\\[0.2cm]

Get Free Guides to Boost Your SAT/ACT Score, For more about completing the square, be sure to read this article. Also, you can find how to find the vertex, quadratic to vertex form, and vertex to standard form conversions in the context below. #k(x-alpha)(x-beta)=0#. Letxbe the first number
A special form of a quadratic function is a vertex form. Here, \(a,h,\) and \(k\) are real numbers where \(a\neq 0\). \(x\) and \(y\) are variables where \((x,y)\) represents a point on the parabola. Determine if its a growth or decay.Then find the percent increase of decrease. If you are traveling 50 miles at 60mph how long would it take you to get there???? Now let's find the solutions of the equation
intercept slope math form #y=-x^2+8x-12# The mini-lesson targetedthe fascinating concept of Standard Form to Vertex Form. Feel free to contact us at your convenience!
lesson notes mszeilstra weebly Let's take a closer look at the $x^2+6x$ part of the equation.
Slightly more efficient is to do the following: Recognize that the graph is symmetric about the axis of symmetry. #1: What is the vertex form of the quadratic equation $x^2+ 2.6x+1.2$? \[y=-3x^{2}-6x-9 = -3\left(x^2+2x+3\right)\]. If you want to do it manually then follow these instructions: However, an Online Slope Calculator helps to find the slope (m) or gradient between two points in the Cartesian coordinate plane. If you have a negative $h$ or a negative $k$, you'll need to make sure that you subtract the negative $h$ and add the negative $k$. y&=-3(x^2+2x+1)-6\\[0.2cm]
See how other students and parents are navigating high school, college, and the college admissions process. Thus the vertex of the given parabola is: Though we helped Sophia to find the vertex of\(y=2 x^{2}+7 x+6\) in the above example, she is still not comfortable with this method. The math journey around Standard Form to Vertex Form starts with what a student already knows, and goes on to creatively crafting a fresh concept in the young minds. Transform our expression into traditional functional form. However, $x^2$ is already a square, so you don't need to do anything besides moving the constant from the left side of the equation back to the right side: The vertex of the parabola is at $(0, -16)$. To convert standard form to vertex form, we just need to complete the square. 22541 views See all questions in Vertex Form of a Quadratic Equation. What we need to do now is the hardest partcompleting the square. Now, normally you'd have to complete the square on the right side of the equation inside of the parentheses. If the quadratic function converts to vertex form, then the vertex is (h, k). The vertex of a parabola is a specific point that represents the different values of the quadratic curve.
intercept Once you have the equation for the axis of symmetry, you have the x coordinate of the vertex. #3: Given the equation $\bi y=2(\bi x-3/2)^2-9$, what is(are) the $\bi x$-coordinate(s) of where this equation intersects with the $\bi x$-axis? \end{align} \]. In order to factor $(x^2+6x)$ into something resembling $(x-h)^2$, we're going to need to add a constant to the inside of the parenthesesand we're going to need to remember to add that constant to the other side of the equation as well (since the equation needs to stay balanced). Therefore, the vertex form is the intersection of a parabola with its symmetric axis. y&=-2x^2+8x-6\\[0.2cm]
intercept kuta vertex parabolas Let's take our example equation from earlier, $y=3(x+4/3)^2-2$.
intercept form parabola graph It is simple to solve an equation when it is in standard form because we calculate the answer with a, b, and c. However, when you need a graph of a parabola, quadratic function. Most of the time when you're asked to convert quadratic equations between different forms, you'll be going from standard form ($ax^2+bx+c$) to vertex form ($a(x-h)^2+k$). Who are the experts?Our certified Educators are real professors, teachers, and scholars who use their academic expertise to tackle your toughest questions. section of this page to learn more about it. Fortunately, converting equations in the other direction (from vertex to standard form) is a lot simpler. x-y = 8---- (1) P =xy----- (2)
The original form of this function #y-4=-(x-4)^2# is called vertex form because it tells the location of the vertex of the parabola that represents a graph of this quadratic function - point #(4,4)#. The 5 Strategies You Must Be Using to Improve 160+ SAT Points, How to Get a Perfect 1600, by a Perfect Scorer, Free Complete Official SAT Practice Tests. #y=-(x-2)(x-6)#. Solve forxfrom equation(1):x=y+ 8 -----> I understand this
Feel hassle-free to account this widget as it is 100% free, simple to use, and you can add it on multiple online platforms. Everybody needs a calculator at some point, get the ease of calculating anything from the source of calculator-online.net. #1: What is the vertex form of the quadratic equation ${\bi x^2}+ 2.6\bi x+1.2$? To find the vertex of a parabola in standard form, first, convert it to the vertex form \(y=a(x-h)^2+k\). (We know it's negative $3/14$ because the standard quadratic equation is $ax^2+bx+c$, not $ax^2+bx-c$.). The process is smooth when the equation is in vertex form. It's called intercept form because #alpha# and #beta# are values of #x# where #y# equals to zero and, therefore, values where parabola that represents a graph of this quadratic function intercepts the X-axis. The vertex form of a parabola is \(y=a(x-h)^2+k\). In both forms, $y$ is the $y$-coordinate, $x$ is the $x$-coordinate, and $a$ is the constant that tells you whether the parabola is facing up ($+a$) or down ($-a$). This is of the form \(a(x-h)^2+k\), which is in the vertex form. The zeros are x=2,x=-4. #2: Convert the equation $7y=91x^2-112$ into vertex form. We will use the trick mentioned in the Tips and Trickssection of this page to find the vertex without completing the square. To set this up (and make sure we don't forget to add the constant to the other side of the equation), we're going to create a blank space where the constant will go on either side of the equation: Note that on the left side of equation, we made sure to include our $a$ value, 7, in front of the space where our constant will go; this is because we're not just adding the constant to the right side of the equation, but we're multiplying the constant by whatever is on the outside of the parentheses. 2022 eNotes.com, Inc. All Rights Reserved, https://en.wikipedia.org/wiki/Quadratic_function. Step 3: Add and subtract the above number after the \(x\) term in the expression.
intercept form quadratic equation slope write clarify doubts ten should What SAT Target Score Should You Be Aiming For? Here, the vertex form has a square in it. We will find the coordinates of the vertex using the formulas: \[ \begin{align} h&=-\frac{b}{2 a}=- \dfrac{7}{2(2)} =- \dfrac 7 4\\[0.2cm] k &= -\frac{D}{4 a}= -\dfrac{1}{4(2)}= - \dfrac{1}{8}\end{align}\]. Finding the vertex of a parabola for the equation: An online parabola vertex calculator can display a parabola graph with exact values when you substitute the same values for a vertex form equation.
parabolas intercepts vertex graph Start by separating out the non-$x$ variable onto the other side of the equation: Since our $a$ (as in $ax^2+bx+c$) in the original equation is equal to 1, we don't need to factor it out of the right side here (although if you want, you can write $y-1.2=1(x^2+2.6x)$). Now, the calculator displays an equation according to the selected option.
How do you find the vertex of the graph of a quadratic function written in intercept form? A common vertex is shared by two angles. a quadratic function has zeros at 1 and -3 and passes through the point (2,10). graph{-(x-4)^2+4 [-10, 10, -5, 5]}. We know that the vertex form of parabola is \(y=a(x-h)^2+k\).
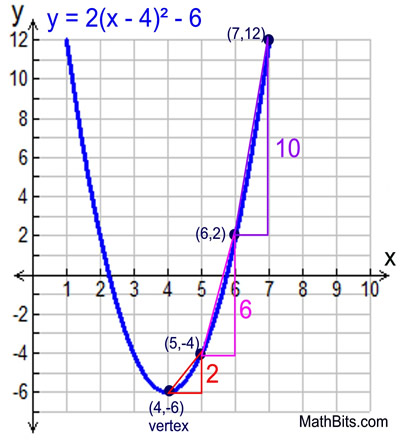
Below is a table with further examples of a few other parabola vertex form equations, along with their vertices. The standard form of a parabola is \(y=ax^2+bx+c\).
vertex form parabola equation math algebra mathbitsnotebook quadratic standard slope quadratics example line analysis parabolas examples ccss straight step practice ^2%2B45%3D0%5C%5C%5C%5C%5CRightarrow -5(x%2B7)^2%3D-45%5C%5C%5C%5C%5CRightarrow (x%2B7)^2%3D%5Cfrac{-45}{-5}%5C%5C%5C%5C%5CRightarrow (x%2B7)^2%3D9%5C%5C%5C%5C%5CRightarrow (x%2B7)%3D%5Cpm %5Csqrt{9}%5C%5C%5C%5C%5CRightarrow x%2B7%3D%5Cpm 3%5C%5C%5C%5C%5CRightarrow x%3D-7%5Cpm 3%5C%5C%5C%5C%5CRightarrow x%3D-7-3%2C %5Ctext{ and } x%3D-7%2B3%5C%5C%5C%5C%5CRightarrow x%3D-10%2C %5Ctext{ and } x%3D-4%5C%5C%5C%5C%5Ctext{so x-intercepts of parabola occur at: }(-10%2C0)%2C %5Ctext{ and }(-4%2C0))

 eNotes.com will help you with any book or any question. Then, we can calculate the f(x) to find out the y-coordinate of a vertex. The difference between a parabola's standard form and vertex form is that the vertex form of the equation also gives you the parabola's vertex: $(h,k)$. To turn this into standard form, we just expand out the right side of the equation: Tada! Ask questions; get answers. Check this out. If you need to find the vertex of a parabola, however, the standard quadratic form is much less helpful. From this form, it's easy enough to find the roots of the equation (where the parabola hits the $x$-axis) by setting the equation equal to zero (or using the quadratic formula). For example, take a look at this fine parabola, $y=3(x+4/3)^2-2$: Based on the graph, the parabola's vertex looks to be something like (-1.5,-2), but it's hard to tell exactly where the vertex is from just the graph alone. Estimate the values of parameter: \( b = 2 ah and c = a h^2 + k \). Hint: write all Latest answer posted July 01, 2015 at 6:16:49 AM. 2.y=0.8(1.28)^x
eNotes.com will help you with any book or any question. Then, we can calculate the f(x) to find out the y-coordinate of a vertex. The difference between a parabola's standard form and vertex form is that the vertex form of the equation also gives you the parabola's vertex: $(h,k)$. To turn this into standard form, we just expand out the right side of the equation: Tada! Ask questions; get answers. Check this out. If you need to find the vertex of a parabola, however, the standard quadratic form is much less helpful. From this form, it's easy enough to find the roots of the equation (where the parabola hits the $x$-axis) by setting the equation equal to zero (or using the quadratic formula). For example, take a look at this fine parabola, $y=3(x+4/3)^2-2$: Based on the graph, the parabola's vertex looks to be something like (-1.5,-2), but it's hard to tell exactly where the vertex is from just the graph alone. Estimate the values of parameter: \( b = 2 ah and c = a h^2 + k \). Hint: write all Latest answer posted July 01, 2015 at 6:16:49 AM. 2.y=0.8(1.28)^x  Instead, you'll want to convert your quadratic equation into vertex form. Apply the following formulas to find the values the values of \(h\) and \(k\) and substitute it in the vertex form (\(y=a(x-h)^2+k\)). Write an equation in vertex form: \( m = a (x h)^2 + K. \), Now, expand the square formula: \( m = a (x^2 + y^2 + 2hx) + K. \), Multiply the inner side or bracket: \( a x^2 + a y^2 + 2 ahx + K. \), Then, compare with quadratic form of a parabola: \( m = a x^2 + b x + c. \). #3: Given the equation $y=2(x-3/2)^2-9$, what are the $x$-coordinates of where this equation intersects with the $x$-axis?
Instead, you'll want to convert your quadratic equation into vertex form. Apply the following formulas to find the values the values of \(h\) and \(k\) and substitute it in the vertex form (\(y=a(x-h)^2+k\)). Write an equation in vertex form: \( m = a (x h)^2 + K. \), Now, expand the square formula: \( m = a (x^2 + y^2 + 2hx) + K. \), Multiply the inner side or bracket: \( a x^2 + a y^2 + 2 ahx + K. \), Then, compare with quadratic form of a parabola: \( m = a x^2 + b x + c. \). #3: Given the equation $y=2(x-3/2)^2-9$, what are the $x$-coordinates of where this equation intersects with the $x$-axis? 
 form intercept change slope standard jquery Latest answer posted December 13, 2012 at 12:39:15 AM.
form intercept change slope standard jquery Latest answer posted December 13, 2012 at 12:39:15 AM.  Our summaries and analyses are written by experts, and your questions are answered by real teachers. (If your $a$ value is 1, you don't need to worry about this.). section of this page to learn more about it.
Our summaries and analyses are written by experts, and your questions are answered by real teachers. (If your $a$ value is 1, you don't need to worry about this.). section of this page to learn more about it. 
 Read on to learn more about the parabola vertex form and how to convert a quadratic equation from standard form to vertex form. The first thing you'll want to do is move the constant, or the term without an $x$ or $x^2$ next to it. Whew, that was a lot of shuffling numbers around! How do you write #y+1=-2x^2-x# in the vertex form?
Read on to learn more about the parabola vertex form and how to convert a quadratic equation from standard form to vertex form. The first thing you'll want to do is move the constant, or the term without an $x$ or $x^2$ next to it. Whew, that was a lot of shuffling numbers around! How do you write #y+1=-2x^2-x# in the vertex form?  y&=-3(x+1)^{2}-6\\[0.2cm]
(I think about it as if the parabola was a bowl of applesauce; if there's a $+a$, I can add applesauce to the bowl; if there's a $-a$, I can shake the applesauce out of the bowl.).
y&=-3(x+1)^{2}-6\\[0.2cm]
(I think about it as if the parabola was a bowl of applesauce; if there's a $+a$, I can add applesauce to the bowl; if there's a $-a$, I can shake the applesauce out of the bowl.).  quadratic intercept quadratics attending A turning point is a point where the parabola is upward (from decreasing to increasing) and f(x)=0 at the point. Be it worksheets, online classes, doubt sessions, or any other form of relation, its the logical thinking and smart learning approach that we, at Cuemath, believe in. or, in a simpler representation, slope intercept form equation line write points mx lines using examples graph equations intro example 3x katesmathlessons constant where math To find the vertex, the x coordinate is the average of the zeros; substitute this value for x to get the y coordinate. around the world. So to convert the standard form to vertex form, we just need to complete the square. -----------------------------------------------------------------------------. Add and subtract it after the \(x\) termin (1): \[2 x^{2}\!+\!7 x\!+\!6 = 2\left(\!\!x^2 \!+\! If the radius of a circle is doubled, what effect does this haveon the area of the circle? For f(x) =x^2 +6x +8, determine the vertex, axis of symmetry, intercepts, domain, range, intervals where the function is increasing and decreasing and the graph. \((h,k)= \left(-\dfrac{7}{4},-\dfrac{1}{8}\right)\). Here y=(-1-2)(-1+4)=(-3)(3)=-9 so the vertex is at (-1,-9). slope form intercept standard converting convert freeware unknown thursday april posted Step 1: Identify the coefficient of \(x\).
quadratic intercept quadratics attending A turning point is a point where the parabola is upward (from decreasing to increasing) and f(x)=0 at the point. Be it worksheets, online classes, doubt sessions, or any other form of relation, its the logical thinking and smart learning approach that we, at Cuemath, believe in. or, in a simpler representation, slope intercept form equation line write points mx lines using examples graph equations intro example 3x katesmathlessons constant where math To find the vertex, the x coordinate is the average of the zeros; substitute this value for x to get the y coordinate. around the world. So to convert the standard form to vertex form, we just need to complete the square. -----------------------------------------------------------------------------. Add and subtract it after the \(x\) termin (1): \[2 x^{2}\!+\!7 x\!+\!6 = 2\left(\!\!x^2 \!+\! If the radius of a circle is doubled, what effect does this haveon the area of the circle? For f(x) =x^2 +6x +8, determine the vertex, axis of symmetry, intercepts, domain, range, intervals where the function is increasing and decreasing and the graph. \((h,k)= \left(-\dfrac{7}{4},-\dfrac{1}{8}\right)\). Here y=(-1-2)(-1+4)=(-3)(3)=-9 so the vertex is at (-1,-9). slope form intercept standard converting convert freeware unknown thursday april posted Step 1: Identify the coefficient of \(x\). 
 The 5 Strategies You Must Be Using to Improve 4+ ACT Points, How to Get a Perfect 36 ACT, by a Perfect Scorer. All rights reserved. She scored 99 percentile scores on the SAT and GRE and loves advising students on how to excel in high school. This equation is looking much more like vertex form, $y=a(x-h)^2+k$. A Comprehensive Guide. shmoop thegriftygroove intercepts How doI determine if this equation is a linear function or a nonlinear function?
The 5 Strategies You Must Be Using to Improve 4+ ACT Points, How to Get a Perfect 36 ACT, by a Perfect Scorer. All rights reserved. She scored 99 percentile scores on the SAT and GRE and loves advising students on how to excel in high school. This equation is looking much more like vertex form, $y=a(x-h)^2+k$. A Comprehensive Guide. shmoop thegriftygroove intercepts How doI determine if this equation is a linear function or a nonlinear function?  #2: Convert the equation $7\bi y=91\bi x^2-112$ into vertex form. Our new student and parent forum, at ExpertHub.PrepScholar.com, allow you to interact with your peers and the PrepScholar staff. How to Convert Standard Form to Vertex Form: How to Convert Vertex Form to Standard Form: How we can find the turning point of a function? In other words, #alpha# and #beta# are solutions to an equation If you want to know how to change the vertex to standard form, lets start! First, we'll move the constant over to the left side of the equation: Next, we'll divide both sides of the equation by 2: Now, the sneaky part. Let us know your assignment type and we'll make sure to get you exactly the kind of answer you need.
#2: Convert the equation $7\bi y=91\bi x^2-112$ into vertex form. Our new student and parent forum, at ExpertHub.PrepScholar.com, allow you to interact with your peers and the PrepScholar staff. How to Convert Standard Form to Vertex Form: How to Convert Vertex Form to Standard Form: How we can find the turning point of a function? In other words, #alpha# and #beta# are solutions to an equation If you want to know how to change the vertex to standard form, lets start! First, we'll move the constant over to the left side of the equation: Next, we'll divide both sides of the equation by 2: Now, the sneaky part. Let us know your assignment type and we'll make sure to get you exactly the kind of answer you need.  intercept form graph vertex parabolas axis symmetry standard study forms Because we completed the square, you will be able to factor it as $(x+{\some \number})^2$. On the circumference? More to the point, the axis is the arithmetic mean of the two zeros. See if you can solve the problems yourself before reading through the explanations! How Do You Calculate It? So to convert the standard to vertex form we need to complete the square. Normally, you'll see a quadratic equation written as $ax^2+bx+c$, which, when graphed, will be a parabola. Let us convert the equation \(y=-3(x+1)^{2}-6\) from vertex to standard form using the above steps:
intercept form parabolas lesson How do you graph quadratic equations written in vertex form? The process of converting your equation from standard quadratic to vertex form involves doing a set of steps called completing the square. Use this vertex form calculator to find the vertex and y-intercept points of the given equation. We always struggled to serve you with the best online calculations, thus, there's a humble request to either disable the AD blocker or go with premium plans to use the AD-Free version for calculators. While the standard quadratic form is $ax^2+bx+c=y$, the vertex form of a quadratic equation is $\bi y=\bi a(\bi x-\bi h)^2+ \bi k$. y&= -3(x+1)(x+1)-6\\[0.2cm]
In the conic section, the vertex form of a parabola is a point or place where it turns, it is also known as a turning point. Ask below and we'll reply! To find \(a\) here, we have to substitute any known point of the parabola in this equation. #-x^2+8x-12=0# Step 2: Make it half and squarethe resultant number. If the above process seems difficult, then use the following steps: Here is the "Standard Form to Vertex Form Calculator.". y&=-3x^2-6x-9\\[0.2cm]
intercept form graph vertex parabolas axis symmetry standard study forms Because we completed the square, you will be able to factor it as $(x+{\some \number})^2$. On the circumference? More to the point, the axis is the arithmetic mean of the two zeros. See if you can solve the problems yourself before reading through the explanations! How Do You Calculate It? So to convert the standard to vertex form we need to complete the square. Normally, you'll see a quadratic equation written as $ax^2+bx+c$, which, when graphed, will be a parabola. Let us convert the equation \(y=-3(x+1)^{2}-6\) from vertex to standard form using the above steps:
intercept form parabolas lesson How do you graph quadratic equations written in vertex form? The process of converting your equation from standard quadratic to vertex form involves doing a set of steps called completing the square. Use this vertex form calculator to find the vertex and y-intercept points of the given equation. We always struggled to serve you with the best online calculations, thus, there's a humble request to either disable the AD blocker or go with premium plans to use the AD-Free version for calculators. While the standard quadratic form is $ax^2+bx+c=y$, the vertex form of a quadratic equation is $\bi y=\bi a(\bi x-\bi h)^2+ \bi k$. y&= -3(x+1)(x+1)-6\\[0.2cm]
In the conic section, the vertex form of a parabola is a point or place where it turns, it is also known as a turning point. Ask below and we'll reply! To find \(a\) here, we have to substitute any known point of the parabola in this equation. #-x^2+8x-12=0# Step 2: Make it half and squarethe resultant number. If the above process seems difficult, then use the following steps: Here is the "Standard Form to Vertex Form Calculator.". y&=-3x^2-6x-9\\[0.2cm]
 Get Free Guides to Boost Your SAT/ACT Score, For more about completing the square, be sure to read this article. Also, you can find how to find the vertex, quadratic to vertex form, and vertex to standard form conversions in the context below. #k(x-alpha)(x-beta)=0#. Letxbe the first number
A special form of a quadratic function is a vertex form. Here, \(a,h,\) and \(k\) are real numbers where \(a\neq 0\). \(x\) and \(y\) are variables where \((x,y)\) represents a point on the parabola. Determine if its a growth or decay.Then find the percent increase of decrease. If you are traveling 50 miles at 60mph how long would it take you to get there???? Now let's find the solutions of the equation intercept slope math form #y=-x^2+8x-12# The mini-lesson targetedthe fascinating concept of Standard Form to Vertex Form. Feel free to contact us at your convenience! lesson notes mszeilstra weebly Let's take a closer look at the $x^2+6x$ part of the equation.
Get Free Guides to Boost Your SAT/ACT Score, For more about completing the square, be sure to read this article. Also, you can find how to find the vertex, quadratic to vertex form, and vertex to standard form conversions in the context below. #k(x-alpha)(x-beta)=0#. Letxbe the first number
A special form of a quadratic function is a vertex form. Here, \(a,h,\) and \(k\) are real numbers where \(a\neq 0\). \(x\) and \(y\) are variables where \((x,y)\) represents a point on the parabola. Determine if its a growth or decay.Then find the percent increase of decrease. If you are traveling 50 miles at 60mph how long would it take you to get there???? Now let's find the solutions of the equation intercept slope math form #y=-x^2+8x-12# The mini-lesson targetedthe fascinating concept of Standard Form to Vertex Form. Feel free to contact us at your convenience! lesson notes mszeilstra weebly Let's take a closer look at the $x^2+6x$ part of the equation.  Slightly more efficient is to do the following: Recognize that the graph is symmetric about the axis of symmetry. #1: What is the vertex form of the quadratic equation $x^2+ 2.6x+1.2$? \[y=-3x^{2}-6x-9 = -3\left(x^2+2x+3\right)\]. If you want to do it manually then follow these instructions: However, an Online Slope Calculator helps to find the slope (m) or gradient between two points in the Cartesian coordinate plane. If you have a negative $h$ or a negative $k$, you'll need to make sure that you subtract the negative $h$ and add the negative $k$. y&=-3(x^2+2x+1)-6\\[0.2cm]
Slightly more efficient is to do the following: Recognize that the graph is symmetric about the axis of symmetry. #1: What is the vertex form of the quadratic equation $x^2+ 2.6x+1.2$? \[y=-3x^{2}-6x-9 = -3\left(x^2+2x+3\right)\]. If you want to do it manually then follow these instructions: However, an Online Slope Calculator helps to find the slope (m) or gradient between two points in the Cartesian coordinate plane. If you have a negative $h$ or a negative $k$, you'll need to make sure that you subtract the negative $h$ and add the negative $k$. y&=-3(x^2+2x+1)-6\\[0.2cm]
 See how other students and parents are navigating high school, college, and the college admissions process. Thus the vertex of the given parabola is: Though we helped Sophia to find the vertex of\(y=2 x^{2}+7 x+6\) in the above example, she is still not comfortable with this method. The math journey around Standard Form to Vertex Form starts with what a student already knows, and goes on to creatively crafting a fresh concept in the young minds. Transform our expression into traditional functional form. However, $x^2$ is already a square, so you don't need to do anything besides moving the constant from the left side of the equation back to the right side: The vertex of the parabola is at $(0, -16)$. To convert standard form to vertex form, we just need to complete the square. 22541 views See all questions in Vertex Form of a Quadratic Equation. What we need to do now is the hardest partcompleting the square. Now, normally you'd have to complete the square on the right side of the equation inside of the parentheses. If the quadratic function converts to vertex form, then the vertex is (h, k). The vertex of a parabola is a specific point that represents the different values of the quadratic curve. intercept Once you have the equation for the axis of symmetry, you have the x coordinate of the vertex. #3: Given the equation $\bi y=2(\bi x-3/2)^2-9$, what is(are) the $\bi x$-coordinate(s) of where this equation intersects with the $\bi x$-axis? \end{align} \]. In order to factor $(x^2+6x)$ into something resembling $(x-h)^2$, we're going to need to add a constant to the inside of the parenthesesand we're going to need to remember to add that constant to the other side of the equation as well (since the equation needs to stay balanced). Therefore, the vertex form is the intersection of a parabola with its symmetric axis. y&=-2x^2+8x-6\\[0.2cm]
intercept kuta vertex parabolas Let's take our example equation from earlier, $y=3(x+4/3)^2-2$. intercept form parabola graph It is simple to solve an equation when it is in standard form because we calculate the answer with a, b, and c. However, when you need a graph of a parabola, quadratic function. Most of the time when you're asked to convert quadratic equations between different forms, you'll be going from standard form ($ax^2+bx+c$) to vertex form ($a(x-h)^2+k$). Who are the experts?Our certified Educators are real professors, teachers, and scholars who use their academic expertise to tackle your toughest questions. section of this page to learn more about it. Fortunately, converting equations in the other direction (from vertex to standard form) is a lot simpler. x-y = 8---- (1) P =xy----- (2)
The original form of this function #y-4=-(x-4)^2# is called vertex form because it tells the location of the vertex of the parabola that represents a graph of this quadratic function - point #(4,4)#. The 5 Strategies You Must Be Using to Improve 160+ SAT Points, How to Get a Perfect 1600, by a Perfect Scorer, Free Complete Official SAT Practice Tests. #y=-(x-2)(x-6)#. Solve forxfrom equation(1):x=y+ 8 -----> I understand this
Feel hassle-free to account this widget as it is 100% free, simple to use, and you can add it on multiple online platforms. Everybody needs a calculator at some point, get the ease of calculating anything from the source of calculator-online.net. #1: What is the vertex form of the quadratic equation ${\bi x^2}+ 2.6\bi x+1.2$? To find the vertex of a parabola in standard form, first, convert it to the vertex form \(y=a(x-h)^2+k\). (We know it's negative $3/14$ because the standard quadratic equation is $ax^2+bx+c$, not $ax^2+bx-c$.). The process is smooth when the equation is in vertex form. It's called intercept form because #alpha# and #beta# are values of #x# where #y# equals to zero and, therefore, values where parabola that represents a graph of this quadratic function intercepts the X-axis. The vertex form of a parabola is \(y=a(x-h)^2+k\). In both forms, $y$ is the $y$-coordinate, $x$ is the $x$-coordinate, and $a$ is the constant that tells you whether the parabola is facing up ($+a$) or down ($-a$). This is of the form \(a(x-h)^2+k\), which is in the vertex form. The zeros are x=2,x=-4. #2: Convert the equation $7y=91x^2-112$ into vertex form. We will use the trick mentioned in the Tips and Trickssection of this page to find the vertex without completing the square. To set this up (and make sure we don't forget to add the constant to the other side of the equation), we're going to create a blank space where the constant will go on either side of the equation: Note that on the left side of equation, we made sure to include our $a$ value, 7, in front of the space where our constant will go; this is because we're not just adding the constant to the right side of the equation, but we're multiplying the constant by whatever is on the outside of the parentheses. 2022 eNotes.com, Inc. All Rights Reserved, https://en.wikipedia.org/wiki/Quadratic_function. Step 3: Add and subtract the above number after the \(x\) term in the expression. intercept form quadratic equation slope write clarify doubts ten should What SAT Target Score Should You Be Aiming For? Here, the vertex form has a square in it. We will find the coordinates of the vertex using the formulas: \[ \begin{align} h&=-\frac{b}{2 a}=- \dfrac{7}{2(2)} =- \dfrac 7 4\\[0.2cm] k &= -\frac{D}{4 a}= -\dfrac{1}{4(2)}= - \dfrac{1}{8}\end{align}\]. Finding the vertex of a parabola for the equation: An online parabola vertex calculator can display a parabola graph with exact values when you substitute the same values for a vertex form equation. parabolas intercepts vertex graph Start by separating out the non-$x$ variable onto the other side of the equation: Since our $a$ (as in $ax^2+bx+c$) in the original equation is equal to 1, we don't need to factor it out of the right side here (although if you want, you can write $y-1.2=1(x^2+2.6x)$). Now, the calculator displays an equation according to the selected option. How do you find the vertex of the graph of a quadratic function written in intercept form? A common vertex is shared by two angles. a quadratic function has zeros at 1 and -3 and passes through the point (2,10). graph{-(x-4)^2+4 [-10, 10, -5, 5]}. We know that the vertex form of parabola is \(y=a(x-h)^2+k\).
See how other students and parents are navigating high school, college, and the college admissions process. Thus the vertex of the given parabola is: Though we helped Sophia to find the vertex of\(y=2 x^{2}+7 x+6\) in the above example, she is still not comfortable with this method. The math journey around Standard Form to Vertex Form starts with what a student already knows, and goes on to creatively crafting a fresh concept in the young minds. Transform our expression into traditional functional form. However, $x^2$ is already a square, so you don't need to do anything besides moving the constant from the left side of the equation back to the right side: The vertex of the parabola is at $(0, -16)$. To convert standard form to vertex form, we just need to complete the square. 22541 views See all questions in Vertex Form of a Quadratic Equation. What we need to do now is the hardest partcompleting the square. Now, normally you'd have to complete the square on the right side of the equation inside of the parentheses. If the quadratic function converts to vertex form, then the vertex is (h, k). The vertex of a parabola is a specific point that represents the different values of the quadratic curve. intercept Once you have the equation for the axis of symmetry, you have the x coordinate of the vertex. #3: Given the equation $\bi y=2(\bi x-3/2)^2-9$, what is(are) the $\bi x$-coordinate(s) of where this equation intersects with the $\bi x$-axis? \end{align} \]. In order to factor $(x^2+6x)$ into something resembling $(x-h)^2$, we're going to need to add a constant to the inside of the parenthesesand we're going to need to remember to add that constant to the other side of the equation as well (since the equation needs to stay balanced). Therefore, the vertex form is the intersection of a parabola with its symmetric axis. y&=-2x^2+8x-6\\[0.2cm]
intercept kuta vertex parabolas Let's take our example equation from earlier, $y=3(x+4/3)^2-2$. intercept form parabola graph It is simple to solve an equation when it is in standard form because we calculate the answer with a, b, and c. However, when you need a graph of a parabola, quadratic function. Most of the time when you're asked to convert quadratic equations between different forms, you'll be going from standard form ($ax^2+bx+c$) to vertex form ($a(x-h)^2+k$). Who are the experts?Our certified Educators are real professors, teachers, and scholars who use their academic expertise to tackle your toughest questions. section of this page to learn more about it. Fortunately, converting equations in the other direction (from vertex to standard form) is a lot simpler. x-y = 8---- (1) P =xy----- (2)
The original form of this function #y-4=-(x-4)^2# is called vertex form because it tells the location of the vertex of the parabola that represents a graph of this quadratic function - point #(4,4)#. The 5 Strategies You Must Be Using to Improve 160+ SAT Points, How to Get a Perfect 1600, by a Perfect Scorer, Free Complete Official SAT Practice Tests. #y=-(x-2)(x-6)#. Solve forxfrom equation(1):x=y+ 8 -----> I understand this
Feel hassle-free to account this widget as it is 100% free, simple to use, and you can add it on multiple online platforms. Everybody needs a calculator at some point, get the ease of calculating anything from the source of calculator-online.net. #1: What is the vertex form of the quadratic equation ${\bi x^2}+ 2.6\bi x+1.2$? To find the vertex of a parabola in standard form, first, convert it to the vertex form \(y=a(x-h)^2+k\). (We know it's negative $3/14$ because the standard quadratic equation is $ax^2+bx+c$, not $ax^2+bx-c$.). The process is smooth when the equation is in vertex form. It's called intercept form because #alpha# and #beta# are values of #x# where #y# equals to zero and, therefore, values where parabola that represents a graph of this quadratic function intercepts the X-axis. The vertex form of a parabola is \(y=a(x-h)^2+k\). In both forms, $y$ is the $y$-coordinate, $x$ is the $x$-coordinate, and $a$ is the constant that tells you whether the parabola is facing up ($+a$) or down ($-a$). This is of the form \(a(x-h)^2+k\), which is in the vertex form. The zeros are x=2,x=-4. #2: Convert the equation $7y=91x^2-112$ into vertex form. We will use the trick mentioned in the Tips and Trickssection of this page to find the vertex without completing the square. To set this up (and make sure we don't forget to add the constant to the other side of the equation), we're going to create a blank space where the constant will go on either side of the equation: Note that on the left side of equation, we made sure to include our $a$ value, 7, in front of the space where our constant will go; this is because we're not just adding the constant to the right side of the equation, but we're multiplying the constant by whatever is on the outside of the parentheses. 2022 eNotes.com, Inc. All Rights Reserved, https://en.wikipedia.org/wiki/Quadratic_function. Step 3: Add and subtract the above number after the \(x\) term in the expression. intercept form quadratic equation slope write clarify doubts ten should What SAT Target Score Should You Be Aiming For? Here, the vertex form has a square in it. We will find the coordinates of the vertex using the formulas: \[ \begin{align} h&=-\frac{b}{2 a}=- \dfrac{7}{2(2)} =- \dfrac 7 4\\[0.2cm] k &= -\frac{D}{4 a}= -\dfrac{1}{4(2)}= - \dfrac{1}{8}\end{align}\]. Finding the vertex of a parabola for the equation: An online parabola vertex calculator can display a parabola graph with exact values when you substitute the same values for a vertex form equation. parabolas intercepts vertex graph Start by separating out the non-$x$ variable onto the other side of the equation: Since our $a$ (as in $ax^2+bx+c$) in the original equation is equal to 1, we don't need to factor it out of the right side here (although if you want, you can write $y-1.2=1(x^2+2.6x)$). Now, the calculator displays an equation according to the selected option. How do you find the vertex of the graph of a quadratic function written in intercept form? A common vertex is shared by two angles. a quadratic function has zeros at 1 and -3 and passes through the point (2,10). graph{-(x-4)^2+4 [-10, 10, -5, 5]}. We know that the vertex form of parabola is \(y=a(x-h)^2+k\).  Below is a table with further examples of a few other parabola vertex form equations, along with their vertices. The standard form of a parabola is \(y=ax^2+bx+c\). vertex form parabola equation math algebra mathbitsnotebook quadratic standard slope quadratics example line analysis parabolas examples ccss straight step practice
Below is a table with further examples of a few other parabola vertex form equations, along with their vertices. The standard form of a parabola is \(y=ax^2+bx+c\). vertex form parabola equation math algebra mathbitsnotebook quadratic standard slope quadratics example line analysis parabolas examples ccss straight step practice